Notas para advertir, entretener y relacionar lo nuevo con lo viejo. Son bienvenidos los comentarios a revmedbuenosaires@gmail.com, o a Basilio A. Kotsias, kotsias@retina.ar
En su libro publicado en 1941, el Brigadier inglés Ralph A. Bagnold (1896-1990)1 señalaba que la escala lineal, desde su aplicación en los templos egipcios había sido aceptada como la única con que la naturaleza construye y trabaja, pero que no era cierta. Apasionado por los mecanismos de transporte de arena y viento en los desiertos y dunas de Libia, Bagnold creó una especialidad que se utiliza en las exploraciones espaciales de reconocimiento de superficies planetarias.
En la fisicoquímica, los logaritmos y su función inversa, la exponencial, aparecen con frecuencia. Allí están las ecuaciones de Nernst para el potencial de reducción y equilibrio iónico y la mecánica estadística de Boltzmann en la dependencia del potencial de los canales iónicos. Están en nuestra vida diaria, desde el pH de una solución, de un cosmético o del agua potable, en la amplitud del volumen sonoro, la tasa de interés en los bancos, en el decaimiento radioactivo, en las diluciones seriadas, en la intensidad sísmica, derretimiento de los glaciares y hasta en el brillo de las estrellas. Uno de los bellos ejemplos de esta función es el caracol Nautilius pompilius en donde el crecimiento de las espiras impulsado por la química y la genética permiten que la criatura conserve su simetría pero cada vez sea más grande (Fig. 1): una espiral equiangular o logarítmica con la distancia entre las espiras que aumentan más rápido que la rotación porque el ángulo alrededor del polo es proporcional al logaritmo del radio vector.
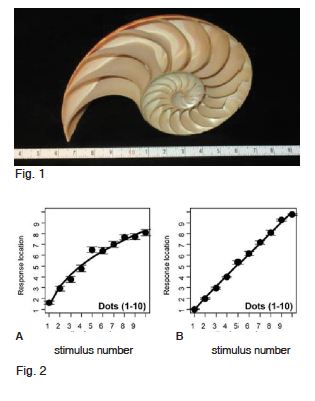
Los estudios sugieren algo más profundo en la interpretación de los números y escalas donde el cerebro humano parece estar preparado para intuir nociones de geometría y apreciar la diferencia numérica desde la niñez1. Los niños del jardín de infantes y primeros años en la escuela ubican los números pequeños separados con un mayor espacio entre ellos que en los mayores, agrupados en el extremo derecho de la escala2. Reforzando esto, aborígenes del Amazonas de la tribu Mundurucu con muy poca o nula conexión con otra sociedad, juzgan las magnitudes en forma no lineal y las grafican por medio de una curva3 (Fig. 2A) en lugar de la lineal en los testigos “educados” (Fig. 2B). Surge la idea de una propiedad innata que la educación transforma en lineal con justificaciones empíricas y teóricas, permitiendo entender el sistema de números, la notación decimal y el álgebra y es una herramienta simple, poderosa y útil para la medición en el cálculo y la geometría.
La idea central es que desde el nacimiento los humanos representan los números en una escala en donde la distancia entre dos números es el resultado de su división y no el resultado de restarlos. La diferencia entre el 1 y el 2 es igual a la que existe entre 1000 y 1001 aunque el significado varía: tener 1 manzana o 2 no es lo mismo que tener 1000 o 1001 de ellas. El mecanismo de esta transformación cerebral está abierto al debate4, 5 pero, de todas maneras, la idea de que la distancia entre los números decrece tiene sentido cuando la juzgamos en términos proporcionales, y ubicamos a los números en una escala de acuerdo al incremento que producen en el número precedente, y cuya suma de esta serie armónica divergente: S=1+(1/2)+(1/3)+(1/4)+(1/5)+ …. ¡Y sorpresa!, resulta similar a la de los logaritmos naturales de esos números. Todo esto sirve para demostrar que la naturaleza no construye en forma lineal sino que parece amar las curvas como las de las dunas de los desiertos.
1. Gaddum, JH. Lognormal distributions. Nature 1945; 156: 463-6. 2. Izard V, Dehaene-Lambertz G, Dehaene S. Distinct cerebral pathways for object identity and number in human infants. PLoS Biol 2008; 6:e11. doi: 10.1371/journal.pbio.0060011.3. Booth JL, Siegler RS. Developmental and individual differences in pure numerical estimation. Dev Psychol 2006; 42:189-201. 4. Dehaene S, Izard V, Spelke E, Pica P. Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science 2008; 320:1217-20. 5. Cicchini GM, Anobile G, Burr DC. Compressive mapping of number to space reflects dynamic encoding mechanisms, not static logarithmic transform. Proc Natl Acad Sci USA 2014; 111:7867-72. 6. Dotan D, Dehaene S. On the origin of logarithmic number-to position mapping. Psychol Rev 2016; 123: 637-66.
